# Import all required libraries
# Data handling and manipulation
import pandas as pd
import numpy as np
# Implementing and selecting models
import statsmodels.api as sm
from sklearn.model_selection import train_test_split, cross_val_score, KFold
from itertools import combinations
from mlxtend.feature_selection import SequentialFeatureSelector as SFS
from sklearn.linear_model import LinearRegression
# For advanced visualizations
import matplotlib.pyplot as plt
import seaborn as sns
# Show computation time
import time
# Increase font size of all Seaborn plot elements
sns.set(font_scale = 1.25)
# Set Seaborn theme
sns.set_theme(style = "white")Regressions I
Lecture 7
University of Arizona
INFO 523 - Spring 2024
Warm up
Announcements
RQ 3 is due today, 11:59pm
HW 3 is due today, 11:59pm
Final project peer-review is Wed Apr 03
Setup
Regressions
Linear regression
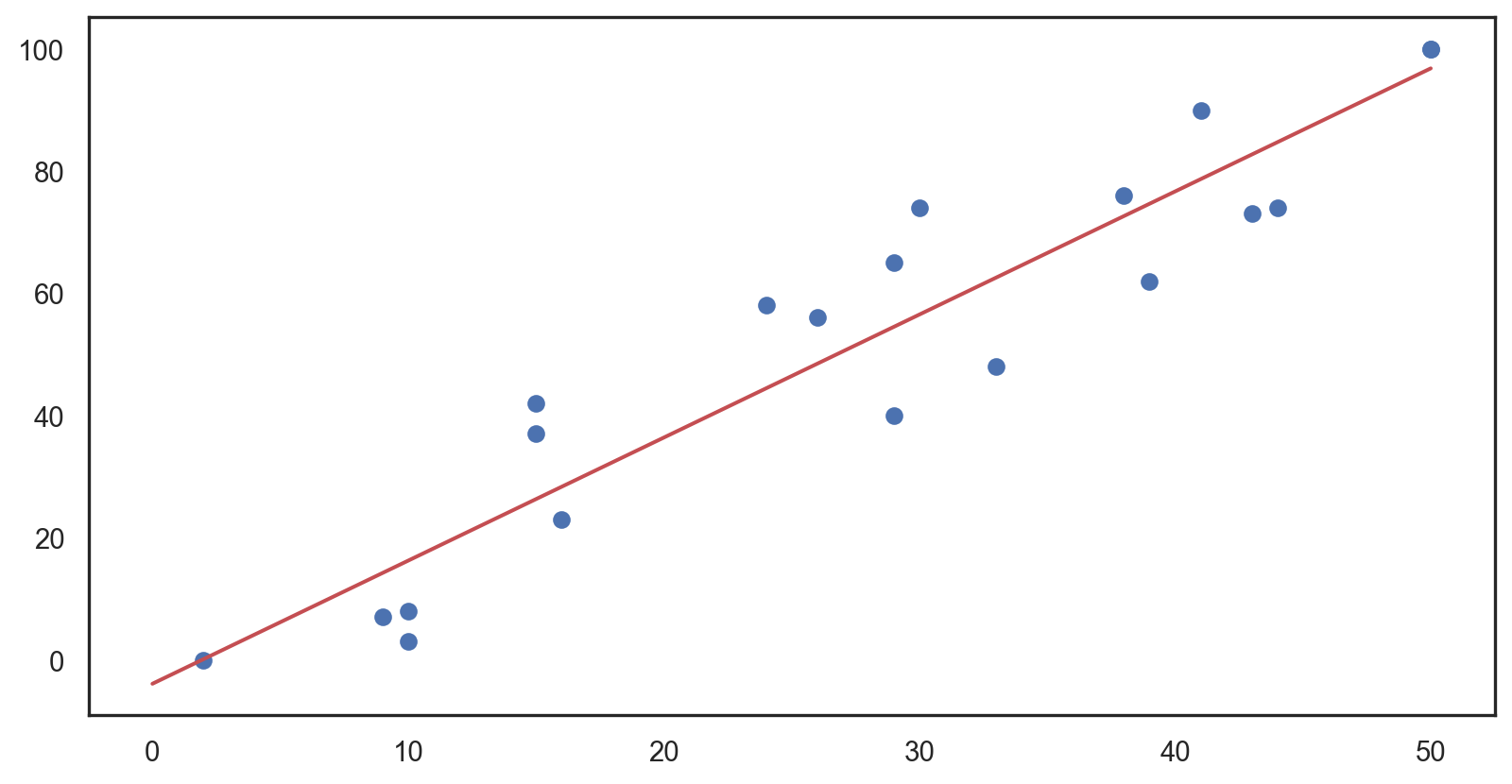
Objective: Minimize the sum of squared differences between observed and predicted.
Model structure:
Yi=β0+β1Xi+ϵi
Yi: Dependent/response variable
Xi: Independent/predictor variable
β0: y-intercept
β1: Slope
ϵi: Random error term, deviation of the real value from predicted
Assumptions: Linearity, independent residuals, constant variance (homoscedasticity), and normally distributed residuals.
Goodness of Fit: Assessed by R2, the proportion of variance in Y explained by X.
Statistical Significance: Tested by t-tests on the coefficients.
Confidence Intervals: Provide a range for the estimated coefficients.
Predictions: Use the model to predict Y for new X values.
Diagnostics: Check residuals for model assumption violations.
Sensitivity: Influenced by outliers which can skew the model.
Applications: Used across various fields for predictive modeling and data analysis.
Assumptions
Linearity
(Linear relationship between Y ~ X)
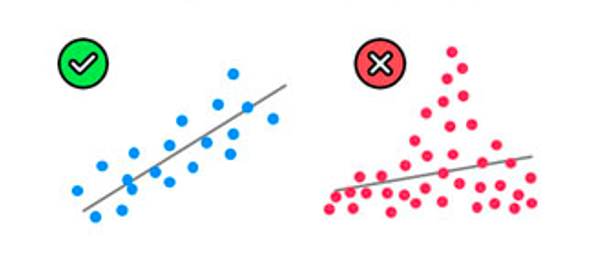
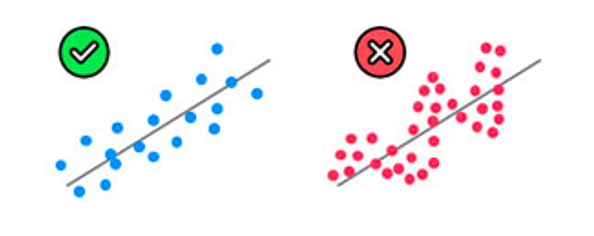
Homoscedasticity
(Equal variance among variables)

Multivartiate Normality
(Normally distributed residuals)

Independence
(Observations are independent)
Lack of Multicollinearity
(Predictors are not correlated)
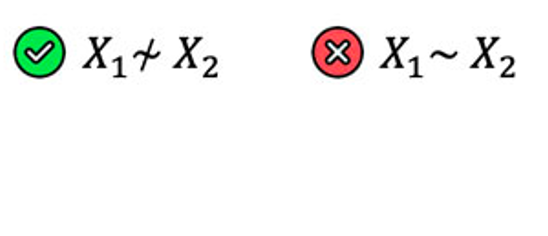
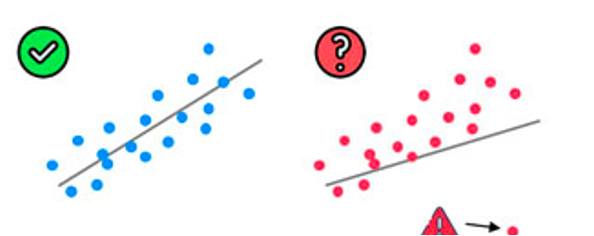
Outlier check
(Technically not an assumption)
Ordinary Least Squares (OLS)
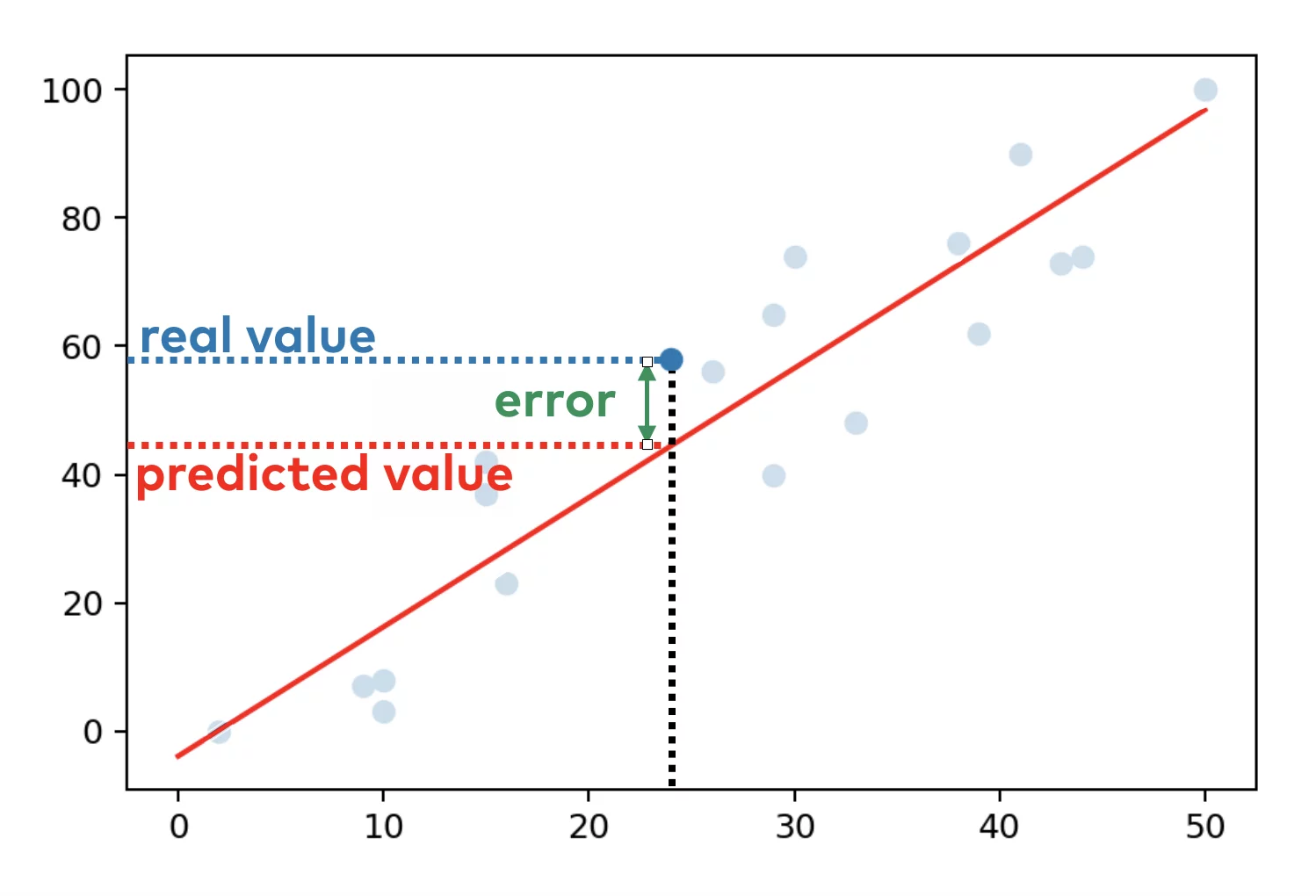
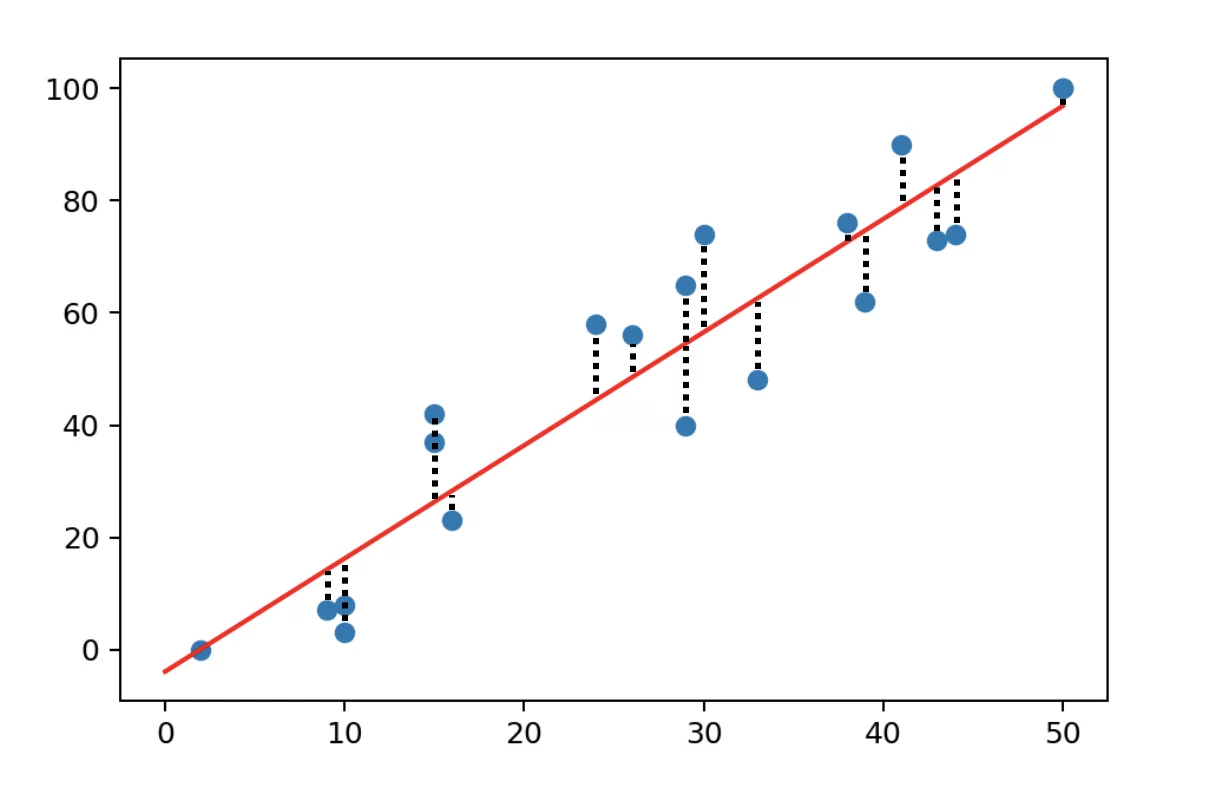
yi=β1xi1+β2xi2+⋯+βpxip+εi
- yi: Dependent variable for the i-th observation.
- β1,β2,…,βp: Coefficients representing the impact of each independent variable.
- xi1,xi1,…,xip: Independent variables for the i-th observation.
- ϵi: Error term for the i-th observation, indicating unexplained variance.
Assessing accuracy of coefficients
Two major methods:
- Standard errors (SE):
Indicate the precision of coefficient estimates; smaller values suggest more precise estimates.
Formula: σˉx≈σx√n
- Confidence Intervals:
Ranges constructed from standard errors that indicate where the true coefficient is likely to fall, typically at a 95% confidence level.
Derived from same method as p-values
Assessing accuracy of model
Four major methods:
- Mean square error (MSE): MSE of a predictor is calculated as the average of the squares of the errors, where the error is the difference between the actual value and the predicted value.
- R-squared (R2): Proportion of variance in the dependent variable explained by the model; closer to 1 indicates a better fit.
- Adjusted R-squared (R2adj): Modified R² that accounts for the number of predictors; useful for comparing models with different numbers of independent variables.
- Residual plots: Visual check for randomness in residuals; patterns may indicate model issues like non-linearity or heteroscedasticity.
In statistics, the mean squared error (MSE) or mean squared deviation (MSD) of an estimator measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. The MSE either assesses the quality of a predictoror of an estimator.
Predictor
MSE=1n∑ni=1(yi−ˆyi)2
yi: the actual values
ˆyi: the predicted values
n: sample size
Define the residuals as ei=yi−fi(forming a vector e).
If ˉy is the observed mean:
ˉy=1n∑ni=1yi
then the variability of the data set can be measured with two sums of squares (SS) formulas:
RSS=∑ni=1(yi−ˆyi)2
TSS=∑ni=1(yi−ˉy)2
R-squared:
R2=1−RSSTSS
Formula R2=1−RSS/dfresTSS/dftot
Key points:
Penalizes Complexity: Adjusts for the number of terms in the model, penalizing the addition of irrelevant predictors.
Comparability: More reliable than R-squared for comparing models with different numbers of independent variables.
Value Range: Can be negative if the model is worse than using just the mean of the dependent variable, whereas R-squared is always between 0 and 1.
- dfres: degrees of freedom of the estimate of the population variance around the model
- dftot: degrees of freedom of the estimate of the population variance around the mean
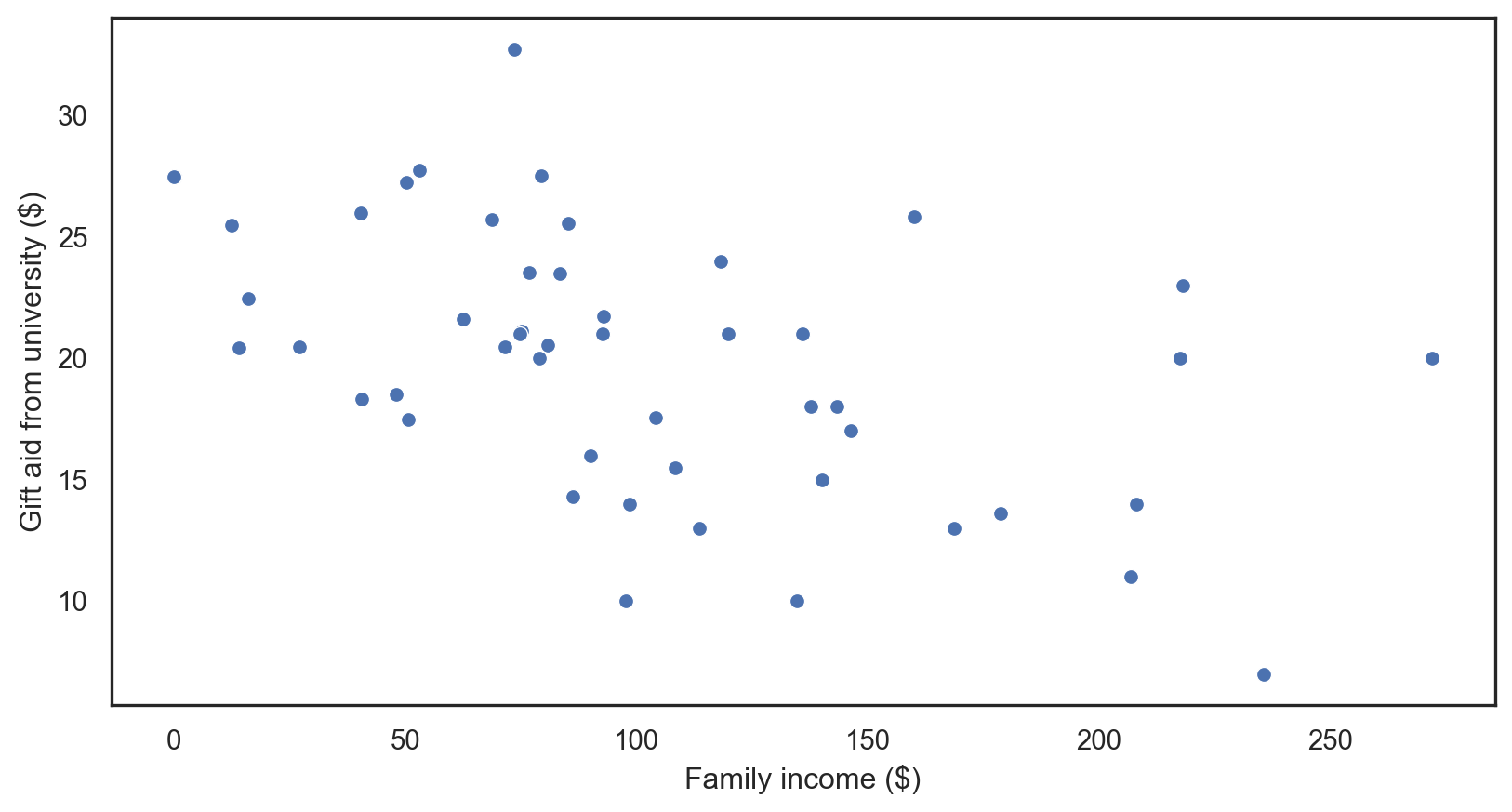
Our data
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 50 entries, 0 to 49
Data columns (total 3 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 family_income 50 non-null float64
1 gift_aid 50 non-null float64
2 price_paid 50 non-null float64
dtypes: float64(3)
memory usage: 1.3 KB| family_income | gift_aid | price_paid | |
|---|---|---|---|
| count | 50.000000 | 50.000000 | 50.000000 |
| mean | 101.778520 | 19.935560 | 19.544440 |
| std | 63.206451 | 5.460581 | 5.979759 |
| min | 0.000000 | 7.000000 | 8.530000 |
| 25% | 64.079000 | 16.250000 | 15.000000 |
| 50% | 88.061500 | 20.470000 | 19.500000 |
| 75% | 137.174000 | 23.515000 | 23.630000 |
| max | 271.974000 | 32.720000 | 35.000000 |
OLS regression: applied
Code
X = elmhurst['family_income'] # Independent variable y = elmhurst['gift_aid'] # Dependent variable X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 42) X_train_with_const = sm.add_constant(X_train) model = sm.OLS(y_train, X_train_with_const).fit() model_summary2 = model.summary2() print(model_summary2)X = elmhurst['family_income'] # Independent variable y = elmhurst['gift_aid'] # Dependent variable X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 42) X_train_with_const = sm.add_constant(X_train) model = sm.OLS(y_train, X_train_with_const).fit() model_summary2 = model.summary2() print(model_summary2)X = elmhurst['family_income'] # Independent variable y = elmhurst['gift_aid'] # Dependent variable X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 42) X_train_with_const = sm.add_constant(X_train) model = sm.OLS(y_train, X_train_with_const).fit() model_summary2 = model.summary2() print(model_summary2)X = elmhurst['family_income'] # Independent variable y = elmhurst['gift_aid'] # Dependent variable X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 42) X_train_with_const = sm.add_constant(X_train) model = sm.OLS(y_train, X_train_with_const).fit() model_summary2 = model.summary2() print(model_summary2)X = elmhurst['family_income'] # Independent variable y = elmhurst['gift_aid'] # Dependent variable X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 42) X_train_with_const = sm.add_constant(X_train) model = sm.OLS(y_train, X_train_with_const).fit() model_summary2 = model.summary2() print(model_summary2)X = elmhurst['family_income'] # Independent variable y = elmhurst['gift_aid'] # Dependent variable X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 42) X_train_with_const = sm.add_constant(X_train) model = sm.OLS(y_train, X_train_with_const).fit() model_summary2 = model.summary2() print(model_summary2)
Results: Ordinary least squares
=================================================================
Model: OLS Adj. R-squared: 0.205
Dependent Variable: gift_aid AIC: 241.3545
Date: 2024-04-25 15:09 BIC: 244.7323
No. Observations: 40 Log-Likelihood: -118.68
Df Model: 1 F-statistic: 11.05
Df Residuals: 38 Prob (F-statistic): 0.00197
R-squared: 0.225 Scale: 23.273
-----------------------------------------------------------------
Coef. Std.Err. t P>|t| [0.025 0.975]
-----------------------------------------------------------------
const 24.5170 1.4489 16.9216 0.0000 21.5839 27.4500
family_income -0.0398 0.0120 -3.3238 0.0020 -0.0640 -0.0156
-----------------------------------------------------------------
Omnibus: 0.057 Durbin-Watson: 2.277
Prob(Omnibus): 0.972 Jarque-Bera (JB): 0.249
Skew: 0.047 Prob(JB): 0.883
Kurtosis: 2.625 Condition No.: 230
=================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the
errors is correctly specified.Code
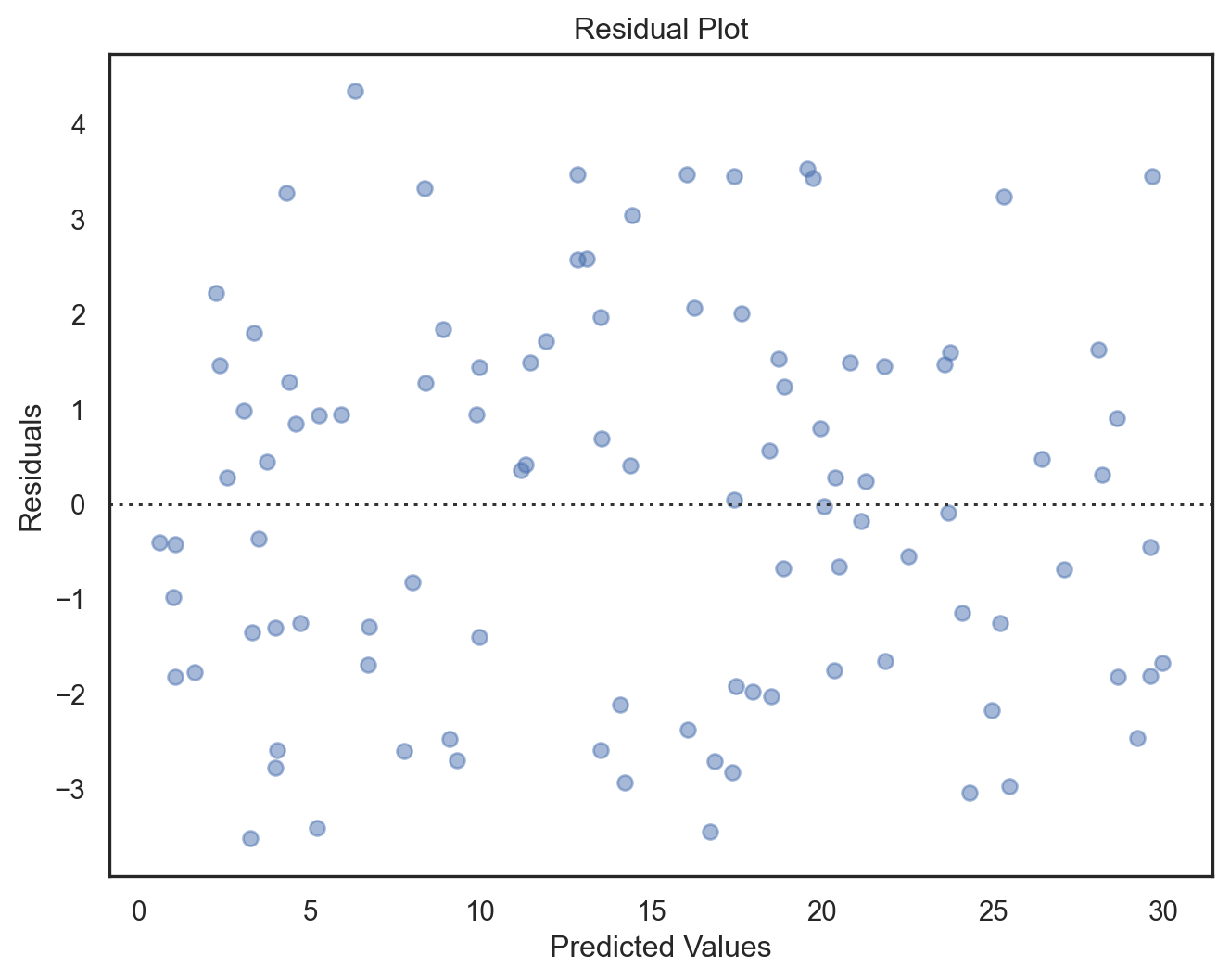
X_test_with_const = sm.add_constant(X_test) predictions = model.predict(X_test_with_const) residuals = y_test - predictions sns.residplot(x = predictions, y = residuals) plt.xlabel('Predicted Values') plt.ylabel('Residuals') plt.title('Residual Plot') plt.show()X_test_with_const = sm.add_constant(X_test) predictions = model.predict(X_test_with_const) residuals = y_test - predictions sns.residplot(x = predictions, y = residuals) plt.xlabel('Predicted Values') plt.ylabel('Residuals') plt.title('Residual Plot') plt.show()X_test_with_const = sm.add_constant(X_test) predictions = model.predict(X_test_with_const) residuals = y_test - predictions sns.residplot(x = predictions, y = residuals) plt.xlabel('Predicted Values') plt.ylabel('Residuals') plt.title('Residual Plot') plt.show()X_test_with_const = sm.add_constant(X_test) predictions = model.predict(X_test_with_const) residuals = y_test - predictions sns.residplot(x = predictions, y = residuals) plt.xlabel('Predicted Values') plt.ylabel('Residuals') plt.title('Residual Plot') plt.show()X_test_with_const = sm.add_constant(X_test) predictions = model.predict(X_test_with_const) residuals = y_test - predictions sns.residplot(x = predictions, y = residuals) plt.xlabel('Predicted Values') plt.ylabel('Residuals') plt.title('Residual Plot') plt.show()
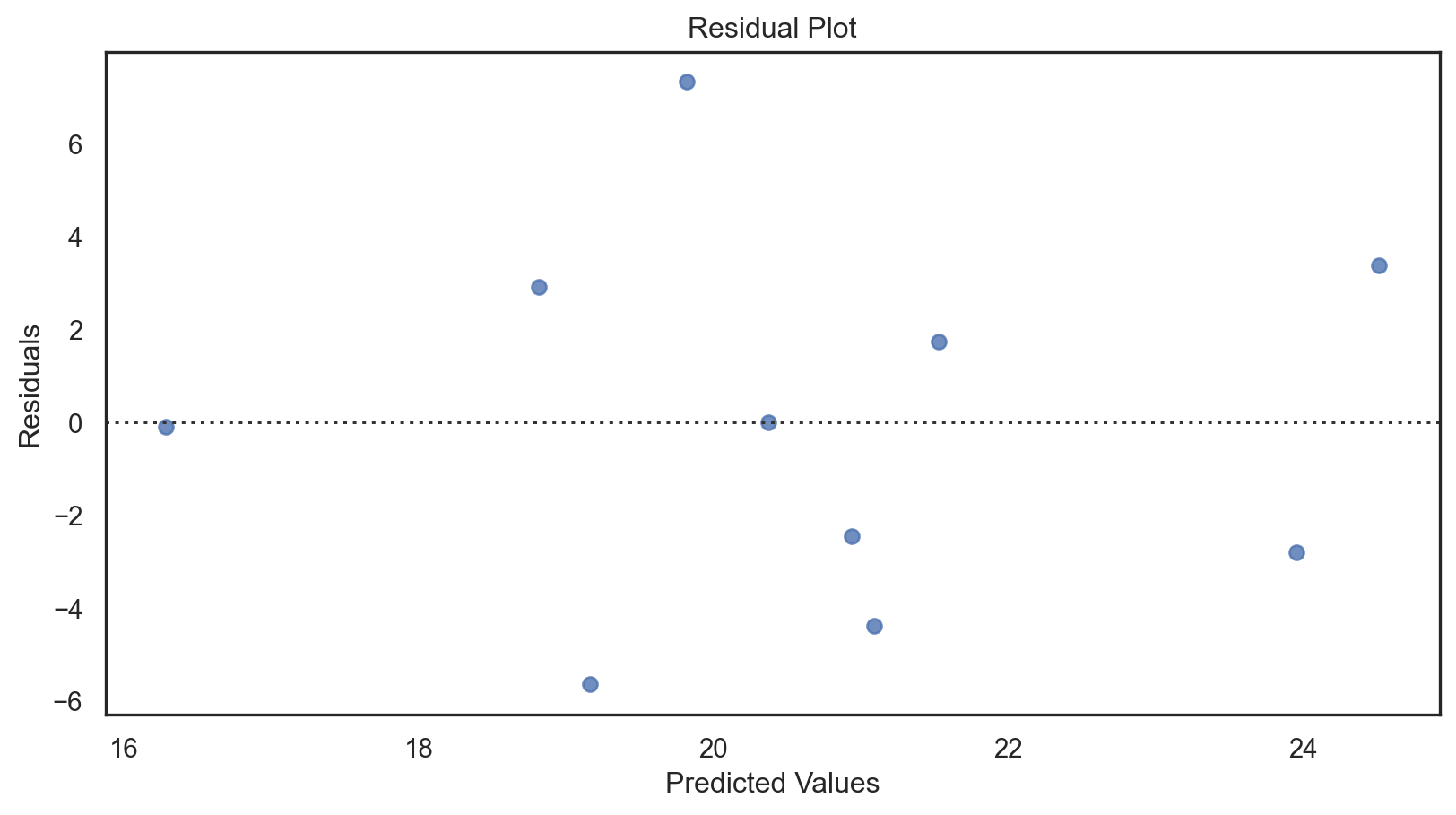
Code
plt.scatter(X_test, y_test, label = 'Data') line_x = np.linspace(X_test.min(), X_test.max(), 100) line_y = model.predict(sm.add_constant(line_x)) plt.plot(line_x, line_y, color = 'red', label = 'OLS Regression Line') plt.xlabel("Family income ($)") plt.ylabel("Gift aid from university ($)") plt.title('OLS Regression Fit') plt.legend() plt.show()plt.scatter(X_test, y_test, label = 'Data') line_x = np.linspace(X_test.min(), X_test.max(), 100) line_y = model.predict(sm.add_constant(line_x)) plt.plot(line_x, line_y, color = 'red', label = 'OLS Regression Line') plt.xlabel("Family income ($)") plt.ylabel("Gift aid from university ($)") plt.title('OLS Regression Fit') plt.legend() plt.show()plt.scatter(X_test, y_test, label = 'Data') line_x = np.linspace(X_test.min(), X_test.max(), 100) line_y = model.predict(sm.add_constant(line_x)) plt.plot(line_x, line_y, color = 'red', label = 'OLS Regression Line') plt.xlabel("Family income ($)") plt.ylabel("Gift aid from university ($)") plt.title('OLS Regression Fit') plt.legend() plt.show()plt.scatter(X_test, y_test, label = 'Data') line_x = np.linspace(X_test.min(), X_test.max(), 100) line_y = model.predict(sm.add_constant(line_x)) plt.plot(line_x, line_y, color = 'red', label = 'OLS Regression Line') plt.xlabel("Family income ($)") plt.ylabel("Gift aid from university ($)") plt.title('OLS Regression Fit') plt.legend() plt.show()plt.scatter(X_test, y_test, label = 'Data') line_x = np.linspace(X_test.min(), X_test.max(), 100) line_y = model.predict(sm.add_constant(line_x)) plt.plot(line_x, line_y, color = 'red', label = 'OLS Regression Line') plt.xlabel("Family income ($)") plt.ylabel("Gift aid from university ($)") plt.title('OLS Regression Fit') plt.legend() plt.show()
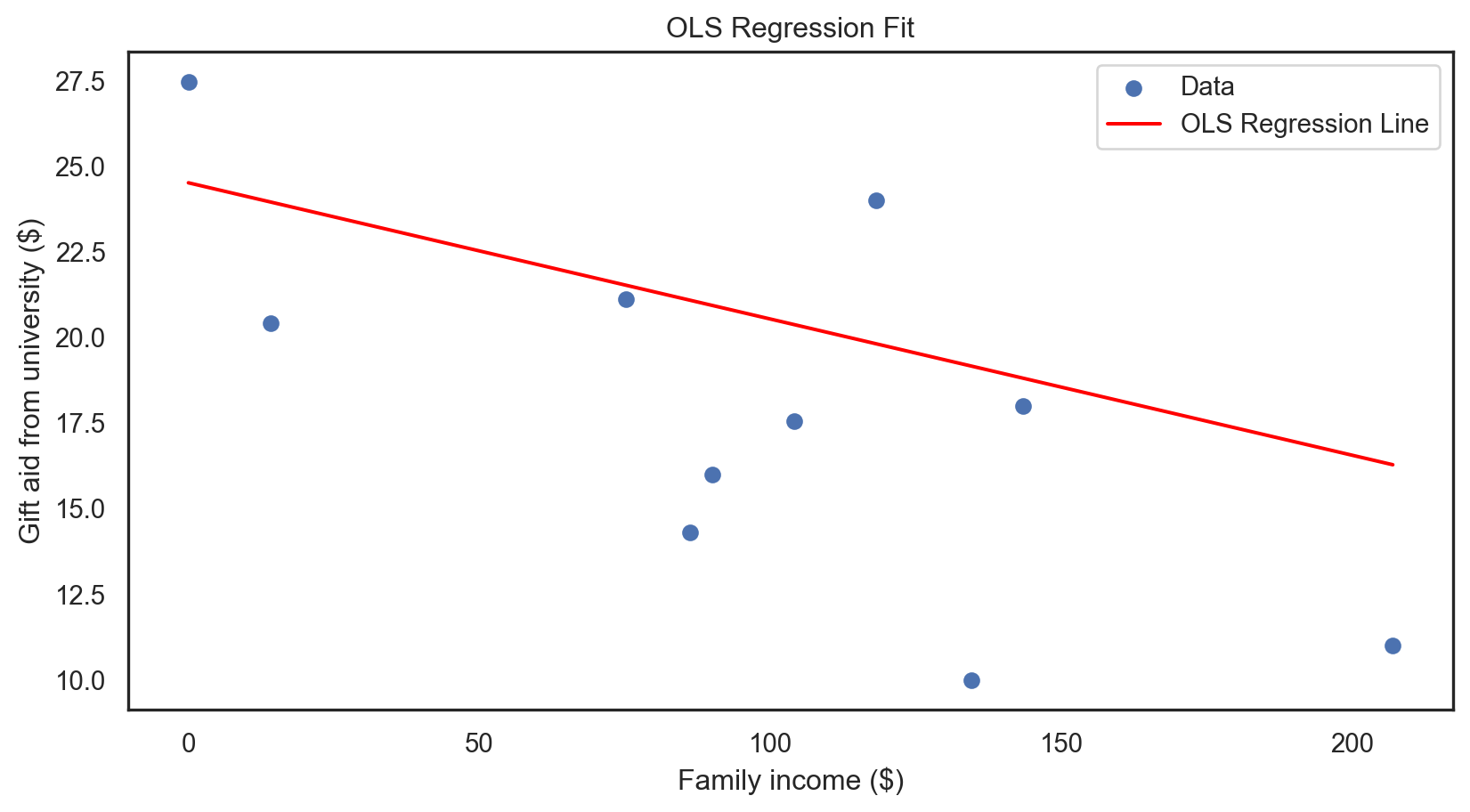
Multiple regression
Multiple regression


Multiple Predictors: more than one predictor variable to predict a response variable.
Model Form: Y=β0+β1X1+β2X2+⋯+βnXn+ϵ , where Y is the response variable, X1,X2,...,Xn are predictor variables, βs are coefficients, and ϵ is the error term.
Coefficient Interpretation: Each coefficient represents the change in the response variable for one unit change in the predictor, holding other predictors constant.
Assumptions: Includes linearity, no perfect multicollinearity, homoscedasticity, independence of errors, and normality of residuals.
Adjusted R-squared: Used to determine the model’s explanatory power, adjusting for the number of predictors.
Multicollinearity Concerns: High correlation between predictor variables can distort the model and make coefficient estimates unreliable.
Interaction Effects: Can be included to see if the effect of one predictor on the response variable depends on another predictor.
Our data
How do factors like debt-to-income ratio, bankruptcy history, and loan term affect the interest rate of a loan?

| emp_title | emp_length | state | homeownership | annual_income | verified_income | debt_to_income | annual_income_joint | verification_income_joint | debt_to_income_joint | ... | sub_grade | issue_month | loan_status | initial_listing_status | disbursement_method | balance | paid_total | paid_principal | paid_interest | paid_late_fees | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | global config engineer | 3.0 | NJ | MORTGAGE | 90000.0 | Verified | 18.01 | NaN | NaN | NaN | ... | C3 | Mar-2018 | Current | whole | Cash | 27015.86 | 1999.33 | 984.14 | 1015.19 | 0.0 |
| 1 | warehouse office clerk | 10.0 | HI | RENT | 40000.0 | Not Verified | 5.04 | NaN | NaN | NaN | ... | C1 | Feb-2018 | Current | whole | Cash | 4651.37 | 499.12 | 348.63 | 150.49 | 0.0 |
| 2 | assembly | 3.0 | WI | RENT | 40000.0 | Source Verified | 21.15 | NaN | NaN | NaN | ... | D1 | Feb-2018 | Current | fractional | Cash | 1824.63 | 281.80 | 175.37 | 106.43 | 0.0 |
| 3 | customer service | 1.0 | PA | RENT | 30000.0 | Not Verified | 10.16 | NaN | NaN | NaN | ... | A3 | Jan-2018 | Current | whole | Cash | 18853.26 | 3312.89 | 2746.74 | 566.15 | 0.0 |
| 4 | security supervisor | 10.0 | CA | RENT | 35000.0 | Verified | 57.96 | 57000.0 | Verified | 37.66 | ... | C3 | Mar-2018 | Current | whole | Cash | 21430.15 | 2324.65 | 1569.85 | 754.80 | 0.0 |
5 rows × 55 columns
| Variable | Description |
|---|---|
interest_rate |
Interest rate on the loan, in an annual percentage. |
verified_income |
Borrower’s income verification: Verified, Source Verified, and Not Verified. |
debt_to_income |
Debt-to-income ratio, which is the percentage of total debt of the borrower divided by their total income. |
credit_util |
The fraction of available credit utilized. |
bankruptcy |
An indicator variable for whether the borrower has a past bankruptcy in their record. This variable takes a value of 1 if the answer is yes and 0 if the answer is no. |
term |
The length of the loan, in months. |
issue_month |
The month and year the loan was issued. |
credit_checks |
Number of credit checks in the last 12 months. |
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 10000 entries, 0 to 9999
Data columns (total 55 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 emp_title 9167 non-null object
1 emp_length 9183 non-null float64
2 state 10000 non-null object
3 homeownership 10000 non-null object
4 annual_income 10000 non-null float64
5 verified_income 10000 non-null object
6 debt_to_income 9976 non-null float64
7 annual_income_joint 1495 non-null float64
8 verification_income_joint 1455 non-null object
9 debt_to_income_joint 1495 non-null float64
10 delinq_2y 10000 non-null int64
11 months_since_last_delinq 4342 non-null float64
12 earliest_credit_line 10000 non-null int64
13 inquiries_last_12m 10000 non-null int64
14 total_credit_lines 10000 non-null int64
15 open_credit_lines 10000 non-null int64
16 total_credit_limit 10000 non-null int64
17 total_credit_utilized 10000 non-null int64
18 num_collections_last_12m 10000 non-null int64
19 num_historical_failed_to_pay 10000 non-null int64
20 months_since_90d_late 2285 non-null float64
21 current_accounts_delinq 10000 non-null int64
22 total_collection_amount_ever 10000 non-null int64
23 current_installment_accounts 10000 non-null int64
24 accounts_opened_24m 10000 non-null int64
25 months_since_last_credit_inquiry 8729 non-null float64
26 num_satisfactory_accounts 10000 non-null int64
27 num_accounts_120d_past_due 9682 non-null float64
28 num_accounts_30d_past_due 10000 non-null int64
29 num_active_debit_accounts 10000 non-null int64
30 total_debit_limit 10000 non-null int64
31 num_total_cc_accounts 10000 non-null int64
32 num_open_cc_accounts 10000 non-null int64
33 num_cc_carrying_balance 10000 non-null int64
34 num_mort_accounts 10000 non-null int64
35 account_never_delinq_percent 10000 non-null float64
36 tax_liens 10000 non-null int64
37 public_record_bankrupt 10000 non-null int64
38 loan_purpose 10000 non-null object
39 application_type 10000 non-null object
40 loan_amount 10000 non-null int64
41 term 10000 non-null int64
42 interest_rate 10000 non-null float64
43 installment 10000 non-null float64
44 grade 10000 non-null object
45 sub_grade 10000 non-null object
46 issue_month 10000 non-null object
47 loan_status 10000 non-null object
48 initial_listing_status 10000 non-null object
49 disbursement_method 10000 non-null object
50 balance 10000 non-null float64
51 paid_total 10000 non-null float64
52 paid_principal 10000 non-null float64
53 paid_interest 10000 non-null float64
54 paid_late_fees 10000 non-null float64
dtypes: float64(17), int64(25), object(13)
memory usage: 4.2+ MB| emp_length | annual_income | debt_to_income | annual_income_joint | debt_to_income_joint | delinq_2y | months_since_last_delinq | earliest_credit_line | inquiries_last_12m | total_credit_lines | ... | public_record_bankrupt | loan_amount | term | interest_rate | installment | balance | paid_total | paid_principal | paid_interest | paid_late_fees | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 9183.000000 | 1.000000e+04 | 9976.000000 | 1.495000e+03 | 1495.000000 | 10000.00000 | 4342.000000 | 10000.00000 | 10000.00000 | 10000.000000 | ... | 10000.000000 | 10000.000000 | 10000.000000 | 10000.000000 | 10000.000000 | 10000.000000 | 10000.000000 | 10000.000000 | 10000.000000 | 10000.000000 |
| mean | 5.930306 | 7.922215e+04 | 19.308192 | 1.279146e+05 | 19.979304 | 0.21600 | 36.760709 | 2001.29000 | 1.95820 | 22.679600 | ... | 0.123800 | 16361.922500 | 43.272000 | 12.427524 | 476.205323 | 14458.916610 | 2494.234773 | 1894.448466 | 599.666781 | 0.119516 |
| std | 3.703734 | 6.473429e+04 | 15.004851 | 7.016838e+04 | 8.054781 | 0.68366 | 21.634939 | 7.79551 | 2.38013 | 11.885439 | ... | 0.337172 | 10301.956759 | 11.029877 | 5.001105 | 294.851627 | 9964.561865 | 3958.230365 | 3884.407175 | 517.328062 | 1.813468 |
| min | 0.000000 | 0.000000e+00 | 0.000000 | 1.920000e+04 | 0.320000 | 0.00000 | 1.000000 | 1963.00000 | 0.00000 | 2.000000 | ... | 0.000000 | 1000.000000 | 36.000000 | 5.310000 | 30.750000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 2.000000 | 4.500000e+04 | 11.057500 | 8.683350e+04 | 14.160000 | 0.00000 | 19.000000 | 1997.00000 | 0.00000 | 14.000000 | ... | 0.000000 | 8000.000000 | 36.000000 | 9.430000 | 256.040000 | 6679.065000 | 928.700000 | 587.100000 | 221.757500 | 0.000000 |
| 50% | 6.000000 | 6.500000e+04 | 17.570000 | 1.130000e+05 | 19.720000 | 0.00000 | 34.000000 | 2003.00000 | 1.00000 | 21.000000 | ... | 0.000000 | 14500.000000 | 36.000000 | 11.980000 | 398.420000 | 12379.495000 | 1563.300000 | 984.990000 | 446.140000 | 0.000000 |
| 75% | 10.000000 | 9.500000e+04 | 25.002500 | 1.515455e+05 | 25.500000 | 0.00000 | 53.000000 | 2006.00000 | 3.00000 | 29.000000 | ... | 0.000000 | 24000.000000 | 60.000000 | 15.050000 | 644.690000 | 20690.182500 | 2616.005000 | 1694.555000 | 825.420000 | 0.000000 |
| max | 10.000000 | 2.300000e+06 | 469.090000 | 1.100000e+06 | 39.980000 | 13.00000 | 118.000000 | 2015.00000 | 29.00000 | 87.000000 | ... | 3.000000 | 40000.000000 | 60.000000 | 30.940000 | 1566.590000 | 40000.000000 | 41630.443684 | 40000.000000 | 4216.440000 | 52.980000 |
8 rows × 42 columns
Our data: preprocessed
loans['credit_util'] = loans['total_credit_utilized'] / loans['total_credit_limit']
loans['bankruptcy'] = (loans['public_record_bankrupt'] != 0).astype(int)
loans['verified_income'] = loans['verified_income'].astype('category').cat.remove_unused_categories()
loans = loans.rename(columns = {'inquiries_last_12m': 'credit_checks'})
loans = loans[['interest_rate', 'verified_income', 'debt_to_income', 'credit_util', 'bankruptcy', 'term', 'credit_checks', 'issue_month']]Multiple regression: applied
Code
X = loans[['verified_income', 'debt_to_income', 'credit_util', 'bankruptcy', 'term', 'credit_checks', 'issue_month']]
y = loans['interest_rate']
X = pd.get_dummies(X, columns = ['verified_income', 'issue_month'], drop_first = True)
X.fillna(0, inplace=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 42)
X_train_with_const = sm.add_constant(X_train)
X_test_with_const = sm.add_constant(X_test)
X_train_with_const = X_train_with_const.astype(int)
X_test_with_const = X_test_with_const.astype(int)
model = sm.OLS(y_train, X_train_with_const).fit()
model_summary2 = model.summary2()
print(model_summary2) Results: Ordinary least squares
==============================================================================
Model: OLS Adj. R-squared: 0.191
Dependent Variable: interest_rate AIC: 46653.7930
Date: 2024-04-25 15:09 BIC: 46723.6650
No. Observations: 8000 Log-Likelihood: -23317.
Df Model: 9 F-statistic: 210.4
Df Residuals: 7990 Prob (F-statistic): 0.00
R-squared: 0.192 Scale: 19.937
------------------------------------------------------------------------------
Coef. Std.Err. t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 4.0713 0.2319 17.5583 0.0000 3.6167 4.5258
debt_to_income 0.0330 0.0033 9.8715 0.0000 0.0265 0.0396
credit_util 3.0409 0.4077 7.4585 0.0000 2.2417 3.8401
bankruptcy 0.5811 0.1543 3.7659 0.0002 0.2786 0.8836
term 0.1445 0.0046 31.5795 0.0000 0.1356 0.1535
credit_checks 0.2122 0.0211 10.0534 0.0000 0.1708 0.2535
verified_income_Source Verified 1.0041 0.1150 8.7304 0.0000 0.7787 1.2296
verified_income_Verified 2.4460 0.1355 18.0457 0.0000 2.1803 2.7117
issue_month_Jan-2018 -0.0778 0.1254 -0.6204 0.5350 -0.3236 0.1680
issue_month_Mar-2018 -0.0178 0.1233 -0.1445 0.8851 -0.2596 0.2239
------------------------------------------------------------------------------
Omnibus: 762.745 Durbin-Watson: 1.958
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1001.147
Skew: 0.820 Prob(JB): 0.000
Kurtosis: 3.562 Condition No.: 398
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is
correctly specified.Code
X_test_with_const = sm.add_constant(X_test)
predictions = model.predict(X_test_with_const)
predictions = pd.to_numeric(predictions, errors='coerce')
residuals = y_test - predictions
residuals = pd.to_numeric(residuals, errors='coerce').fillna(0)
# Plotting the residuals
sns.residplot(x = predictions, y = residuals)
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')
plt.show()
Model optimization
Three major methods:
- AIC (Akaike Information Criterion): a measure of the relative quality of a statistical model for a given set of data. Lower and fewer parameters = better.
- AIC=2k−2ln(L), where k is the number of parameters, and L is the likelihood of the model.
- BIC (Bayesian Information Criterion): a criterion for model selection based on the likelihood of the model. Lower and fewer parameters = better.
- BIC=kln(n)−2ln(L), where k is the number of parameters, n is the sample size, and L is the likelihood of the model
- Cross-Validation: a statistical method used for assessing how the results of a predictive model will generalize to an independent data set.
- Most common method is k-Fold Cross Validation
Pros:
Balanced Approach: AIC balances model fit with complexity, reducing overfitting.
Comparative Utility: Suitable for comparing models on the same dataset.
Widespread Acceptance: Commonly used and recognized in statistical analysis.
Versatile: Applicable across various types of statistical models.
Cons:
Relative Measurement: Only provides a comparative metric and doesn’t indicate absolute model quality.
Risk of Underfitting: Penalizing complex models may lead to underfitting.
Sample Size Sensitivity: Its effectiveness can vary with the size of the dataset.
Assumption of Large Sample: Infinite sample size assumption is impractical.
No Probabilistic Interpretation: Lacks a direct probabilistic meaning, unlike some other statistical measures.
Pros:
Penalizes Complexity: Penalizes complexity, preventing overfitting.
Good for Large Data: The penalty term is more significant in larger datasets.
Model Comparison: Useful for comparing different models on the same dataset.
Widely Recognized: Commonly used in statistical model selection.
Cons:
Relative, Not Absolute: Only provides a comparative metric and doesn’t indicate absolute model quality.
Can Favor Simpler Models: Penalizing complex models may lead to underfitting.
Sample Size Dependent: The effectiveness of BIC is influenced by sample size.
Assumes Correct Model is in Set: Assumes that the true model is given.
Lacks Probabilistic Meaning: Lacks a direct probabilistic meaning, unlike some other statistical measures.
Pros:
Robustness: Provides a more accurate measure of out-of-sample accuracy.
Prevents Overfitting: Helps in detecting overfitting by evaluating model performance on unseen data.
Versatile: Can be used with any predictive modeling technique.
Tuning Hyperparameters: Useful for selecting the best model hyperparameters.
Cons:
Computationally Intensive: Can be slow with large datasets and complex models.
Data Requirements: Requires a sufficient amount of data to partition into meaningful subsets.
Variance: Results can be sensitive to the way in which data is divided.
No Single Best Model: only provides an estimation of how well a model type will perform.
Model selection
Model selection
The task of selecting a model from among various candidates on the basis of performance criterion to choose the best one.
Two major methods:
- Best subset selection: Evaluate all combinations, choose by a criterion - e.g., lowest RSS or highest R2adj
- Stepwise selection: Forward Selection or Backward Selection
Best subset selection
Definition
Best Subset Selection is a statistical method used in regression analysis to select a subset of predictors that provides the best fit for the response variable.
It involves:
Considering All Possible Predictor Subsets: For p predictors, all possible combinations (totaling 2p) of these predictors are considered.
Fitting a Model for Each Subset: A regression model is fitted for each subset of predictors.
Selecting the Best Model: The best model is selected based on a criterion that balances fit and complexity, such as the lowest Residual Sum of Squares (RSS) or the highest R2adj (or AIC, BIC).
For each subset, the model is given by:
Y=β0+∑i∈SβiXi+ϵ
Y: Response variable.
β0: Intercept.
βi: Coefficients for predictors.
Xi: Predictor variables.
ϵ: Error term.
S: Set of indices of selected predictors.
The quality of each model is assessed using a criterion like:
RSS=∑ni=1(yi−ˆyi)2
…or R2adj,AIC,BIC
Pros:
Comprehensive Approach: Evaluates all possible combinations of predictors, ensuring a thorough search.
Flexibility: Can be used with various selection criteria and types of regression models.
Intuitive: Provides a clear framework for model selection.
Cons:
Computational Intensity: The number of models to evaluate grows exponentially with the number of predictors, making it computationally demanding.
Overfitting Risk: May lead to overfit models, especially when the number of observations is not significantly larger than the number of predictors.
Model Selection Complexity: Requires careful choice and interpretation of model selection criteria to balance between model fit and complexity.
Stepwise selection (both types)
Definition
Stepwise selection is a method used in regression analysis to select predictor variables. There are two main types:
Forward Selection:
Starts with no predictor variables in the model.
Iteratively adds the variable that provides the most significant model improvement.
Continues until no significant improvement is made by adding more variables.
Backward Selection:
Begins with all candidate predictor variables.
Iteratively removes the least significant variable (that least worsens the model).
Continues until removing more variables significantly worsens the model.
The criteria for adding or removing a variable are usually based on statistical tests like the F-test or p-values:
Forward selection (adding a variable)
F=(RSS0−RSS1)/p1RSS1/(n−p0−1)
- RSS0 is the Residual Sum of Squares of the current model.
- RSS1 is the Residual Sum of Squares with the additional variable.
- p1 is the number of predictors in the new model.
- n is the number of observations.
- p0 is the number of predictors in the current model.
Backward selection (removing a variable)
Similar criteria but in reverse, considering the increase in RSS or the p-values of the coefficients.
Pros:
Simplicity: More straightforward and computationally less intensive than Best Subset Selection.
Flexibility: Can be adapted to various criteria for entering and removing variables.
Practical: Useful with multicollinearity and large sets of potential predictors.
Cons:
Arbitrary Choices: Depends on the order of variables and the specific entry and removal criteria.
Local Optima: Might not find the best possible model as it doesn’t evaluate all possible combinations.
Overfitting Risk: Especially in datasets with many variables relative to the number of observations.
Statistical Issues: Stepwise methods can inflate the significance of variables and do not account for the search process in assessing the fit.
Best Subset Selection: applied
Code
X = loans[['verified_income', 'debt_to_income', 'credit_util', 'bankruptcy', 'term', 'credit_checks', 'issue_month']]
y = loans['interest_rate']
X = pd.get_dummies(X, columns = ['verified_income', 'issue_month'], drop_first = True)
X.fillna(0, inplace=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 42)
X_train_with_const = sm.add_constant(X_train)
X_test_with_const = sm.add_constant(X_test)
X_train_with_const = X_train_with_const.astype(int)
X_test_with_const = X_test_with_const.astype(int)
model = sm.OLS(y_train, X_train_with_const).fit()
model_summary2 = model.summary2()
print(model_summary2) Results: Ordinary least squares
==============================================================================
Model: OLS Adj. R-squared: 0.191
Dependent Variable: interest_rate AIC: 46653.7930
Date: 2024-04-25 15:09 BIC: 46723.6650
No. Observations: 8000 Log-Likelihood: -23317.
Df Model: 9 F-statistic: 210.4
Df Residuals: 7990 Prob (F-statistic): 0.00
R-squared: 0.192 Scale: 19.937
------------------------------------------------------------------------------
Coef. Std.Err. t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 4.0713 0.2319 17.5583 0.0000 3.6167 4.5258
debt_to_income 0.0330 0.0033 9.8715 0.0000 0.0265 0.0396
credit_util 3.0409 0.4077 7.4585 0.0000 2.2417 3.8401
bankruptcy 0.5811 0.1543 3.7659 0.0002 0.2786 0.8836
term 0.1445 0.0046 31.5795 0.0000 0.1356 0.1535
credit_checks 0.2122 0.0211 10.0534 0.0000 0.1708 0.2535
verified_income_Source Verified 1.0041 0.1150 8.7304 0.0000 0.7787 1.2296
verified_income_Verified 2.4460 0.1355 18.0457 0.0000 2.1803 2.7117
issue_month_Jan-2018 -0.0778 0.1254 -0.6204 0.5350 -0.3236 0.1680
issue_month_Mar-2018 -0.0178 0.1233 -0.1445 0.8851 -0.2596 0.2239
------------------------------------------------------------------------------
Omnibus: 762.745 Durbin-Watson: 1.958
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1001.147
Skew: 0.820 Prob(JB): 0.000
Kurtosis: 3.562 Condition No.: 398
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is
correctly specified.def best_subset_selection(X, y):
results = []
for k in range(1, len(X.columns) + 1):
for combo in combinations(X.columns, k):
X_subset = sm.add_constant(X[list(combo)].astype(int))
model = sm.OLS(y, X_subset).fit()
results.append({'model': model, 'predictors': combo})
return results
subset_results = best_subset_selection(X_train, y_train)best_aic = np.inf
best_model_1 = None
for result in subset_results:
if result['model'].aic < best_aic:
best_aic = result['model'].aic
best_model_1 = result
print("Best Model Predictors:", best_model_1['predictors'])
print("Best Model AIC:", best_aic.round(2))Best Model Predictors: ('debt_to_income', 'credit_util', 'bankruptcy', 'term', 'credit_checks', 'verified_income_Source Verified', 'verified_income_Verified')
Best Model AIC: 46650.23best_bic = np.inf
best_model_2 = None
for result in subset_results:
if result['model'].bic < best_bic:
best_bic = result['model'].bic
best_model_2 = result
print("Best Model Predictors:", best_model_2['predictors'])
print("Best Model BIC:", best_bic.round(2))Best Model Predictors: ('debt_to_income', 'credit_util', 'bankruptcy', 'term', 'credit_checks', 'verified_income_Source Verified', 'verified_income_Verified')
Best Model BIC: 46706.13best_r_sq_adj = -np.inf
best_model_3 = None
for result in subset_results:
if result['model'].rsquared_adj > best_r_sq_adj:
best_r_sq_adj = result['model'].rsquared_adj
best_model_3 = result
print("Best Model Predictors:", best_model_3['predictors'])
print("Best Model Adjusted R-squared:", best_r_sq_adj.round(2))Best Model Predictors: ('debt_to_income', 'credit_util', 'bankruptcy', 'term', 'credit_checks', 'verified_income_Source Verified', 'verified_income_Verified')
Best Model Adjusted R-squared: 0.19Step-wise selection: applied
Code
X = loans[['verified_income', 'debt_to_income', 'credit_util', 'bankruptcy', 'term', 'credit_checks', 'issue_month']]
y = loans['interest_rate']
X = pd.get_dummies(X, columns = ['verified_income', 'issue_month'], drop_first = True)
X.fillna(0, inplace=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 42)
X_train_with_const = sm.add_constant(X_train)
X_test_with_const = sm.add_constant(X_test)
X_train_with_const = X_train_with_const.astype(int)
X_test_with_const = X_test_with_const.astype(int)
model = sm.OLS(y_train, X_train_with_const).fit()
model_summary2 = model.summary2()
print(model_summary2) Results: Ordinary least squares
==============================================================================
Model: OLS Adj. R-squared: 0.191
Dependent Variable: interest_rate AIC: 46653.7930
Date: 2024-04-25 15:09 BIC: 46723.6650
No. Observations: 8000 Log-Likelihood: -23317.
Df Model: 9 F-statistic: 210.4
Df Residuals: 7990 Prob (F-statistic): 0.00
R-squared: 0.192 Scale: 19.937
------------------------------------------------------------------------------
Coef. Std.Err. t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 4.0713 0.2319 17.5583 0.0000 3.6167 4.5258
debt_to_income 0.0330 0.0033 9.8715 0.0000 0.0265 0.0396
credit_util 3.0409 0.4077 7.4585 0.0000 2.2417 3.8401
bankruptcy 0.5811 0.1543 3.7659 0.0002 0.2786 0.8836
term 0.1445 0.0046 31.5795 0.0000 0.1356 0.1535
credit_checks 0.2122 0.0211 10.0534 0.0000 0.1708 0.2535
verified_income_Source Verified 1.0041 0.1150 8.7304 0.0000 0.7787 1.2296
verified_income_Verified 2.4460 0.1355 18.0457 0.0000 2.1803 2.7117
issue_month_Jan-2018 -0.0778 0.1254 -0.6204 0.5350 -0.3236 0.1680
issue_month_Mar-2018 -0.0178 0.1233 -0.1445 0.8851 -0.2596 0.2239
------------------------------------------------------------------------------
Omnibus: 762.745 Durbin-Watson: 1.958
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1001.147
Skew: 0.820 Prob(JB): 0.000
Kurtosis: 3.562 Condition No.: 398
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is
correctly specified.Code
lr = LinearRegression()
# Initialize SequentialFeatureSelector (SFS) for forward selection
sfs = SFS(lr,
k_features = 'best', # Select the best number of features based on criterion
forward = True, # Forward selection
floating = False,
scoring = 'neg_mean_squared_error', # Using negative MSE as scoring criterion
cv = 0) # No cross-validation
# Fit SFS on the training data
sfs.fit(X_train, y_train)
# Get the names of the selected features
selected_features = list(sfs.k_feature_names_)
# Convert the DataFrame to numeric to ensure all features are numeric
X_train = X_train.apply(pd.to_numeric, errors='coerce').fillna(0)
X_test = X_test.apply(pd.to_numeric, errors='coerce').fillna(0)
# Select the features identified by forward selection
X_train_selected = X_train[selected_features]
# Fit the final Linear Regression model using selected features
final_model = lr.fit(X_train_selected, y_train)
# For AIC, BIC, and adjusted R-squared, use statsmodels
X_train_selected_with_const = sm.add_constant(X_train_selected)
# Ensure data type consistency
X_train_selected_with_const = X_train_selected_with_const.astype(float)
# Fit the OLS model
model_sm = sm.OLS(y_train, X_train_selected_with_const).fit()
# Output the results
print("Forward Selection Results")
print("Selected predictors:", selected_features)
print("AIC:", model_sm.aic.round(3))
print("BIC:", model_sm.bic.round(3))
print("Adjusted R-squared:", model_sm.rsquared_adj.round(3))Forward Selection Results
Selected predictors: ['debt_to_income', 'credit_util', 'bankruptcy', 'term', 'credit_checks', 'verified_income_Source Verified', 'verified_income_Verified', 'issue_month_Jan-2018', 'issue_month_Mar-2018']
AIC: 46034.53
BIC: 46104.402
Adjusted R-squared: 0.251Code
# Initialize the linear regression model
lr = LinearRegression()
# Initialize SequentialFeatureSelector (SFS) for forward selection
sfs = SFS(lr,
k_features = 'best', # Select the best number of features based on criterion
forward = False, # Forward selection
floating = False,
scoring = 'neg_mean_squared_error', # Using negative MSE as scoring criterion
cv = 0) # No cross-validation
# Fit SFS on the training data
sfs.fit(X_train, y_train)
# Get the names of the selected features
selected_features = list(sfs.k_feature_names_)
# Convert the DataFrame to numeric to ensure all features are numeric
X_train = X_train.apply(pd.to_numeric, errors='coerce').fillna(0)
X_test = X_test.apply(pd.to_numeric, errors='coerce').fillna(0)
# Select the features identified by forward selection
X_train_selected = X_train[selected_features]
# Fit the final Linear Regression model using selected features
final_model = lr.fit(X_train_selected, y_train)
# For AIC, BIC, and adjusted R-squared, use statsmodels
X_train_selected_with_const = sm.add_constant(X_train_selected)
# Ensure data type consistency
X_train_selected_with_const = X_train_selected_with_const.astype(float)
# Fit the OLS model
model_sm = sm.OLS(y_train, X_train_selected_with_const).fit()
# Output the results
print("Backward Selection Results")
print("Selected predictors:", selected_features)
print("AIC:", model_sm.aic.round(3))
print("BIC:", model_sm.bic.round(3))
print("Adjusted R-squared:", model_sm.rsquared_adj.round(3))Backward Selection Results
Selected predictors: ['debt_to_income', 'credit_util', 'bankruptcy', 'term', 'credit_checks', 'verified_income_Source Verified', 'verified_income_Verified', 'issue_month_Jan-2018', 'issue_month_Mar-2018']
AIC: 46034.53
BIC: 46104.402
Adjusted R-squared: 0.251Cross validation
Code
def best_subset_cv(X, y, max_features=5):
best_score = np.inf
best_subset = None
# Limiting the number of features for computational feasibility
for k in range(1, max_features + 1):
for subset in combinations(X.columns, k):
# Define the model
model = LinearRegression()
# Perform k-fold cross-validation
kf = KFold(n_splits = 5, shuffle = True, random_state = 42)
cv_scores = cross_val_score(model, X[list(subset)], y, cv = kf, scoring = 'neg_mean_squared_error')
# Compute the average score
score = -np.mean(cv_scores) # Convert back to positive MSE
# Update the best score and subset
if score < best_score:
best_score = score
best_subset = subset
return best_subset, best_score
# Start timing
start_time = time.time()
# Assuming X and y are already defined and preprocessed
best_subset, best_score = best_subset_cv(X, y)
# End timing
end_time = time.time()
# Calculate duration
duration = end_time - start_time
print("Best Subset:", best_subset)
print("Best CV Score (MSE):", best_score)
print("Computation Time: {:.2f} seconds".format(duration))Best Subset: ('credit_util', 'term', 'credit_checks', 'verified_income_Source Verified', 'verified_income_Verified')
Best CV Score (MSE): 18.664618422927752
Computation Time: 3.48 secondsCode
# Initialize the linear regression model
lr = LinearRegression()
# Initialize SequentialFeatureSelector for forward selection with cross-validation
sfs = SFS(lr,
k_features = 'best', # 'best' or specify a number with ('1, 10') for range
forward=True,
floating=False,
scoring = 'neg_mean_squared_error',
cv = KFold(n_splits = 5, shuffle = True, random_state = 42))
# Start timing
start_time = time.time()
# Fit SFS on the training data
sfs.fit(X, y)
# End timing
end_time = time.time()
# Calculate duration
duration = end_time - start_time
# Get the names of the selected features
selected_features = list(sfs.k_feature_names_)
print("Selected predictors (forward selection):", selected_features)
print("Computation Time: {:.2f} seconds".format(duration))Selected predictors (forward selection): ['debt_to_income', 'credit_util', 'bankruptcy', 'term', 'credit_checks', 'verified_income_Source Verified', 'verified_income_Verified']
Computation Time: 0.62 secondsCode
# Convert the DataFrame to numeric to ensure all features are numeric
X_train = X_train.apply(pd.to_numeric, errors = 'coerce').fillna(0)
X_test = X_test.apply(pd.to_numeric, errors = 'coerce').fillna(0)
# Select the features identified by forward selection
X_train_selected = X_train[selected_features]
# Fit the final Linear Regression model using selected features
final_model = lr.fit(X_train_selected, y_train)
# For AIC, BIC, and adjusted R-squared, use statsmodels
X_train_selected_with_const = sm.add_constant(X_train_selected)
# Ensure data type consistency
X_train_selected_with_const = X_train_selected_with_const.astype(float)
# Fit the OLS model
model_sm = sm.OLS(y_train, X_train_selected_with_const).fit()
# Model results
model_summary2 = model_sm.summary2()
print("Forward selection best fit:\n")
print(model_summary2)Forward selection best fit:
Results: Ordinary least squares
============================================================================
Model: OLS Adj. R-squared: 0.251
Dependent Variable: interest_rate AIC: 46030.6466
Date: 2024-04-25 15:09 BIC: 46086.5442
No. Observations: 8000 Log-Likelihood: -23007.
Df Model: 7 F-statistic: 384.2
Df Residuals: 7992 Prob (F-statistic): 0.00
R-squared: 0.252 Scale: 18.448
----------------------------------------------------------------------------
Coef. Std.Err. t P>|t| [0.025 0.975]
----------------------------------------------------------------------------
const 2.1781 0.2216 9.8311 0.0000 1.7438 2.6125
debt_to_income 0.0214 0.0032 6.5925 0.0000 0.0150 0.0277
credit_util 4.7592 0.1794 26.5247 0.0000 4.4075 5.1109
bankruptcy 0.4028 0.1486 2.7109 0.0067 0.1115 0.6940
term 0.1493 0.0044 33.8811 0.0000 0.1406 0.1579
credit_checks 0.2238 0.0203 11.0250 0.0000 0.1840 0.2636
verified_income_Source Verified 0.9396 0.1106 8.4934 0.0000 0.7228 1.1565
verified_income_Verified 2.5107 0.1304 19.2581 0.0000 2.2551 2.7663
----------------------------------------------------------------------------
Omnibus: 908.105 Durbin-Watson: 1.953
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1279.631
Skew: 0.884 Prob(JB): 0.000
Kurtosis: 3.843 Condition No.: 242
============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is
correctly specified.Conclusions
OLS regression is a great baseline model to compare against
Falls victim to collinearity, overly complex models
- Hence selection methods with model assessment
Best subset selection can overfit easier than stepwise selection
Stepwise selection is faster
Stepwise inflates Type I error with multiple testing…
Live coding: Indoor air pollution
| variable | class | description |
|---|---|---|
| Entity | character | Country name |
| Code | character | Country code |
| Year | double | Year |
| access_clean_perc | double | Access to clean fuels and technologies for cooking (% of population) |
| variable | class | description |
|---|---|---|
| Entity | character | The country |
| Code | character | Country code |
| Year | double | Year |
| access_clean_perc | double | % of population with access to clean cooking fuels |
| GDP | double | GDP per capita, PPP (constant 2017 international $) |
| popn | double | Country population |
| Continent | character | Continent the country resides on |
| variable | class | description |
|---|---|---|
| Entity | character | The country |
| Code | character | Country code |
| Year | double | Year |
| Death_Rate_ASP | double | Cause of death related to air pollution from solid fuels, standardized |
Live coding
Code
from sklearn.impute import SimpleImputer
from feature_engine.imputation import CategoricalImputer
# Read in data
fuel_access = pd.read_csv('data/fuel_access.csv')
fuel_gdp = pd.read_csv('data/fuel_gdp.csv')
death_source = pd.read_csv('data/death_source.csv')
# Select relevant columns and rename for consistency if needed
fuel_access = fuel_access[['Entity', 'Year', 'access_clean_perc']]
fuel_gdp = fuel_gdp[['Entity', 'Year', 'GDP', 'popn']]
death_source = death_source[['Entity', 'Year', 'Death_Rate_ASP']]
# Ensure 'Year' is an integer
fuel_access['Year'] = fuel_access['Year'].astype(int)
fuel_gdp['Year'] = fuel_gdp['Year'].astype(int)
death_source['Year'] = death_source['Year'].astype(int)
# Merge datasets on 'Entity' and 'Year'
merged_data = pd.merge(fuel_access, fuel_gdp, on = ['Entity', 'Year'], how = 'inner')
merged_data = pd.merge(merged_data, death_source, on = ['Entity', 'Year'], how = 'inner')
# Check for missing values
print(merged_data.isnull().sum())
# Handle missing values if necessary (e.g., fill with mean or median, or drop)
num_imputer = SimpleImputer(strategy = 'mean') # or 'median'
numerical_cols = merged_data.select_dtypes(include = ['int64', 'float64']).columns.tolist()
merged_data[numerical_cols] = num_imputer.fit_transform(merged_data[numerical_cols])
merged_data.dropna()
merged_data['Entity'] = pd.factorize(merged_data['Entity'])[0]
# Final check for data types and missing values
print(merged_data.info())
print(merged_data.isnull().sum())
# Optional: Standardize/normalize numerical columns if necessary
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
numerical_columns = ['access_clean_perc', 'GDP', 'popn']
merged_data[numerical_columns] = scaler.fit_transform(merged_data[numerical_columns])
merged_data.to_csv()
# Define the predictor variables and the response variable
X = merged_data.drop(['Death_Rate_ASP'], axis = 1) # Assuming 'Death_Rate_ASP' is the response variable
y = merged_data['Death_Rate_ASP']
# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 42)
# Initialize LinearRegression model
lr = LinearRegression()
# Initialize SequentialFeatureSelector for forward selection with cross-validation
sfs = SFS(lr,
k_features = 'best', # 'best' or specify a number with ('1, 10') for range
forward = True, # Forward selection
floating = False, # Set to True for stepwise selection
scoring = 'neg_mean_squared_error', # Using negative MSE as scoring criterion
cv = KFold(n_splits = 5, shuffle = True, random_state = 42)) # 5-fold cross-validation
# Fit SFS on the training data
sfs.fit(X_train, y_train)
# Get the names of the selected features
selected_features = list(sfs.k_feature_names_)
# Fit the final Linear Regression model using selected features
final_model = lr.fit(X_train[selected_features], y_train)
# Evaluate the model performance on the test set
from sklearn.metrics import mean_squared_error
y_pred = final_model.predict(X_test[selected_features])
mse = mean_squared_error(y_test, y_pred)
print("Selected predictors (forward selection):", selected_features)
print("Test MSE:", mse)
# Extracting predictor variables (X) and the target variable (y)
X = merged_data[selected_features]
Y = merged_data['Death_Rate_ASP']
# Adding a constant for the intercept term
X = sm.add_constant(X)
# Fit the regression model
model = sm.OLS(y, X).fit()
model_summary = model.summary2()
print(model_summary)